The Sticking Points in Modeling Tires

Tires are perhaps the least well understood parts of road-going vehicles, despite the fact that they are one of the most studied. Obviously, since they are typically the only part of a car in contact with the ground (if everything is working right), their behavior is critical in determining how a car handles, how well it grips the road, and so ultimately, how fast it can go. It has been said that if horses complained, the pneumatic tire would have been invented in ancient times. But it took until the 1800’s and the invention of the human-powered bicycle before it was discovered that an inflated tube of air (thank you, John Dunlop) covered by vulcanized rubber (thank you, Charles Goodyear) was a darn sight better at rolling across the ground than a wooden hoop covered with a strip of iron. Maybe if the ancients had invented them, rubber tires would be better understood by now. I like to joke that I’ve spent my entire adult professional life studying tires, with a few other odd assignments thrown in. That’s what it feels like, anyway, since everything else seems pretty straightforward by comparison. Needless to say, most people, when they hear that my specialty is tire physics, tend to turn and walk (or run) away. So I couldn’t believe my good fortune when Steve asked if I would write a blog post about the tire model I’ve been working on. This might take a while, so grab a sandwich, or better yet, a strong cup of coffee, and read on:

What is a tire model and why do we need one? A tire model is a collection of mathematical formulas, along with a bunch of numbers to plug into those formulas, that when given some basic information about how fast and in which direction a tire is going, what it’s contacting and at what angle, can spit out the forces that the tire exerts on the car. That’s pretty much it. There are a bunch of other force models needed for a racing simulation as well: the aero model—the forces that air is exerting on the car; spring and damper models—the forces that are exerted by the suspension elements; engine and drivetrain model—the forces that spin the drive wheels; brake model—the forces that stop the wheels from spinning; gravity—a gloriously simple force (from a racing sim’s point of view) that makes things fall and hit the ground. When we know all these forces, we can plug them into a complicated version of Newton’s F=ma (force = mass times acceleration) equation, and voila, we get the car’s and all of its component parts’ accelerations.

It’s important to be able to figure out how moving things accelerate, since what we really want to know at the end of all the math is where all those moving things are at a particular instant (like the instant we draw a pretty picture from the cockpit of an iRacing car). To know where things are at any instant, we need to know where they were a short time ago (their positions), and how fast they were moving between then and now (their velocities). If we know how fast they were moving a short time ago, and we can figure out their accelerations between then and now, then we can do a pretty good job of figuring out their velocities between then and now, and so we can figure out where they are now (at least we can make a pretty informed guess). If this all sounds kind of circular, like we need to know where we are in order to know where we are, then you are understanding it perfectly. Two things save us: one, the fact that in our universe stuff doesn’t teleport around like in Star Trek (in other words, positions don’t suddenly change in unpredictable ways, at least for stuff bigger than elementary particles), and two, the velocity of stuff doesn’t change unless a force is acting on it. The ancients didn’t have that second one quite right. It took thousands of years to figure that out, so don’t feel bad if this is making your head spin.

Tires are perhaps the least well understood parts of road-going vehicles, despite the fact that they are one of the most studied.

So this is why we need the force models for sim racing. They give us the accelerations we need (how much the velocities change). We take those accelerations, add them to the car’s and components’ velocities, take those velocities, add them to the car’s and components’ positions, and repeat, a zillion times a second. Every once in a while we draw a picture on screen with the car and all its parts in the correct positions (and with all the other cars and their components in the correct positions). That’s basically it, anyway. We need to do these calculations many times per second because, while the positions and velocities don’t change very fast (not in a thousandth of a second, anyway), the forces can change very rapidly. To get an accurate simulation, we need to compute those forces really, really frequently. We also need to have good models for the forces—that is, the models need to produce the correct forces in any given situation. Most of the forces are surprisingly simple, or at least they can be modeled fairly simply, and any additional complexities (for example, due to temperature) can be handled fairly easily. The two main exceptions to this are aerodynamics and tires, and of the two, tires are more difficult to model.

It turns out that almost all the forces depend primarily on the positions and velocities of the car and its parts. For example, the force exerted by a spring is a fairly constant multiple of how far it is compressed (or stretched). The force exerted by a damper (shock absorber) is a fairly simple function of how fast the damper is being compressed (bump) or expanded (rebound). Aerodynamic forces, while being fairly complex in origin, can be neatly computed from the air speed, air density and a small number of coefficients (fancy term for numbers) that depend only on the orientation of the car relative to the moving air. Gravity is ridiculously simple, always exerting a fixed force in a fixed direction (downward).

The forces exerted by a tire are not so simple, unfortunately. They depend on the position and velocity of the wheel on which the tire is mounted, as well as its angle relative to the ground (its camber). They also depend on the type of surface it’s touching (grass, concrete, asphalt, etc.), the shape of the tire carcass, the tread rubber compound properties, the inflation pressure, the tire temperature (many temperatures, really, around and throughout the tire), the amount of tread rubber wear, the temperature of the road surface, how heavily the tire is compressed into the surface (the load), how fast the wheel is spinning, even the small amount that the tread belt is deflected away from its usual position by these very tire forces! Let’s not even start on surfaces covered with various lubricants like water, coolant, oil, sand, etc.

Gathering real-world data for the iRacing tire model – Dave Kaemmer checks a tire on Calspan’s Tire Industry Research Facility test rig.

Any attempt to measure tire forces inevitably runs into the problem that all these variables are changing all the time. It becomes very difficult to determine just which property of a tire is having which effect on the overall force generated. As you take a tire and steer it on a tire tester, the surface temperature climbs rapidly and heat begins conducting into the tread, changing its characteristics, plus the carcass deflects, which changes the effective steering angle and camber angle. If you try to see what happens at large sliding angles, the tire wears away rapidly, and the temperature skyrockets (producing a lot of noise and smoke, which is pretty cool, by the way). This is not helpful when trying to come up with a good tire model.

There are a couple different ways to attack this problem. One is to measure the forces generated by a tire in as many different configurations as you have the time and money to do (different speeds, loads, pressures, etc.), and come up with “mathematical curve fits” that pass through the measured data as best they can. This is called an “empirical” model, empirical meaning based on observation or experiment. The other way is to try and come up with a theory that predicts what the tire forces would be in all these different configurations. Ideally, such a theory would only need a few basic measurements, and would produce accurate forces in many different situations. This is called a “theoretical” or “physically-based” model.

There are examples of both that have been used in automotive tire simulation for decades. The most well-known empirical model is Pacejka’s “Magic Formula” (that really is what it’s called by PhD’s in the field!), which can give very good results, especially when combined with “Tire Data Nondimensionalization”, which is a method for reducing the many possible tire force curves at different loads into a couple of curves, which can then be modeled with the Magic Formula. There have been many refinements and improvements over the years to this model, and now tire companies will often identify a tire with its “Pacejka coefficients”, the numbers to plug into the Magic Formula to obtain the tire force curves. The refinements have led to models that account for pressure, load and temperature changes, in addition to other improvements. Pure theoretical tire models such as “The Brush Model”, and the “Stretched String Model” have tended to be a bit simpler, and are used more to explain why the empirical models’ curves look the way they do than to predict what those curves will be exactly.

I’ve been talking a lot about “tire force curves” without much explanation. Let’s introduce a picture:

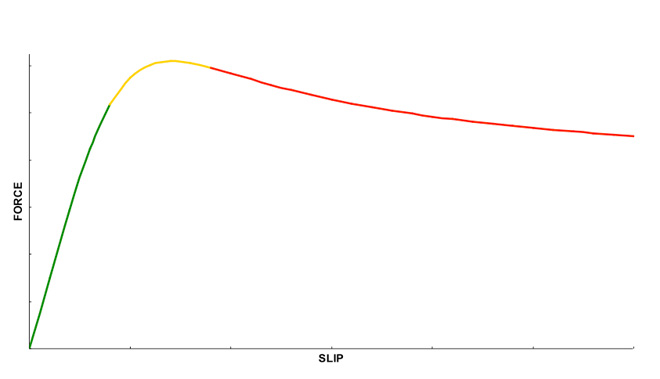
There are several different force curves that we’re interested in with a tire, but this is the important one, and it serves to illustrate a number of things. Plus you probably only have one cup of coffee, and time is running out on me. What you see here is a graph of a tire’s force parallel to the road surface versus a quantity called “slip”. This parallel force could be forward or backward (acceleration or braking), which is called “longitudinal”; it could be sideways (cornering), called “lateral”; or it could be a combination of both together. This curve has roughly the same shape no matter which direction we’re talking about, basically. Slip is a measure of the difference in speed between the tire carcass and the road surface. In the longitudinal direction, the slip is usually referred to as “percent slip”, or % slip. If a rear wheel is spinning at a speed where the tire carcass is travelling at 110 mph, but the car’s speed over the road is just 100 mph, then the tire is operating at 10% slip. In the lateral case, if the car is travelling 100 mph, but it is cornering hard and facing left at a 5 degree angle to its direction of travel, the tire is operating at a “5 degree slip angle”. In both cases, the tire appears to be “slipping” across the road, but in fact the tread rubber is just being stretched when it is in contact with the ground, and then it snaps back into place when it leaves the ground at the back of the “contact patch”. When the slip exceeds a certain amount (as you move to the right on the graph), the contact patch does start sliding (usually near the back of the contact area where the rubber is stretched the most), soon afterwards the force reaches a peak, and then starts falling as the tire’s slip increases still further.

This is just one representative curve which might be the correct curve for a given tire in one particular situation. The difficulty is that as conditions change (and they change very rapidly, all the time) the correct curve changes size and shape. As you drive through a corner, you might travel up one curve, and come back on a different one, because the temperature of the tire has changed, for example. So we need to figure out how and why these curves change. The force versus slip curve has certain characteristics that do stay mostly the same, so let’s look at it more carefully.

Any attempt to measure tire forces inevitably runs into the problem that all these variables are changing all the time

Note that there are three main zones in this force curve: 1) the linear zone in green, when turning the steering wheel more makes the car turn more (i.e. more slip = more force)—where we should always be when driving on public roads, 2) the limit zone in yellow, where the steering wheel becomes just a braking device, the tire starts to squeal happily, and racers make their living (more slip = no real change in force), and 3) the scary zone to the right in red, which is exciting, but not fast, and much rubber is disappearing from the tire surface (more slip = less force). We have discovered over the years from a lot of driver feedback in the simulation that the width of the limit zone and the steepness of the scary zone as you fall into it have a dramatic effect on the “drivability” of a car, and whether or not the tire model feels like a real tire. In order for a racing simulation to properly reproduce the handling characteristics of race cars, you need a tire model that reproduces all three zones well.

Right away, this becomes a problem. The reason is that pretty much nobody is all that interested in the scary zone; they mostly want to avoid it (except for the alternate universe of drifting). Even when testing tires, the scary zone just does too much damage to the tires and so it’s very expensive to test there. Hence there’s very little scary data. If you look at enough measured tire force curves, you’ll see that most of them don’t even extend into the scary zone. When they do, you’ll notice that while empirical curve fits can be really good in the linear and even the limit zones, they don’t really fit the data well in the scary zone. But they don’t need to, for most purposes. No tire company can sell their tires using the pitch, “Our tires have really good scary handling.” They can sell them based on how good the wet skid resistance is, since that is a number required to be tested for all passenger tires that are sold. So unlike most of the scary zone, there is a lot of data for the far right, lowest part of the scary zone, which is where wet skid resistance is measured (tire locked up, sliding on wet pavement). But even that is of little help for tire modeling, since the force at that point is as much a function of the pavement surface as of the tire itself. Also, water dramatically changes what that zone looks like, so all that data doesn’t help on a nice, dry, sunny day.

It gets even worse when we consider that the limit zone (the racer’s office) depends on what is happening in the scary zone. This is because what’s really going on in the limit zone is that the tire is doing both some of its linear thing (stretching the tread rubber), and some of its scary thing (whatever that is) at the same time. The limit zone is just a result of the mixing of the linear and scary zones as we increase the slip. So if we don’t really understand the scary zone, we don’t really understand the limit zone either. Up until not too long ago, the scary zone was keeping me up at night. However, when we did tire measurements last year at a tire test facility, we went ahead and destroyed quite a few tires with different constructions and tread compounds in order to see what they did at very large slip angles and at a bunch of different speeds, loads, and pressures. We were able to get some good scary data. I have been digesting that ever since, and am happy to say that I have come up with a model that is both based on some sound theories, and that produces curves that look like our measured data, which is no small thing, since the data is all over the place!

The other good news is that the linear zone is measured and studied a lot, and although it’s pretty complicated (it still depends on load, pressure, camber, tread rubber characteristics, tire carcass shape and stiffness, tread pattern, tread temperature, tread wear, speed, and some other things), it is possible to break it down into understandable pieces, and make some progress toward a theoretical model. That is what I have been doing, on and off, for quite a while now. So I think I have a good theoretical model for all three zones.

Why not just use an empirical model and be done with it? Wouldn’t that be easier? Well, it would be easier to code up the model, but it’s much more complicated to tweak and tune it so it has the right characteristics in all sorts of conditions (different loads, pressures, temperatures, etc.) Empirical models work well when the conditions can be considered to be fixed, as they might be for a passenger car with the recommended pressures travelling at highway speeds and below. But they become unwieldy in the racing environment, with large temperature changes, pressure changes, aerodynamic downforce and high loads from high-speed, high-banked tracks, along with the need to model curb hits well, and so on. There are just too many different things to measure, and it would be too expensive in terms of tires and time to test them in all necessary conditions. A decent theoretical model, though, should give reasonable responses even when the tire is doing crazy stuff, which on a race track is a lot of the time.

At the end of the day, what does all this mean? Well, I hope it means that once I finish this up, driving a race car on iRacing will be even more like the real thing, and the job of getting the tires right for each car will be a lot easier. That in turn will allow us to improve some of the other force models, as well. And that will continue to give us all more insight into what’s going on out there on the racetrack, increasing our enjoyment of the world’s greatest sport!

You may also like...

Recommended

eNASCAR College iRacing Series returns with Spring Semester in January 2025; Paint Contest announced

Recommended

iRacing Downshift #60: 2024 Recap and Holiday Show

Recommended

Popular World of Outlaws: Dirt Racing 24 Gold Edition Coming to PC via Steam in 2025

Recommended

Logan Rumsey reclaims points lead with second World of Outlaws Pro Series victory at Knoxville